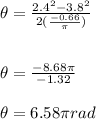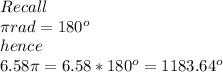Answer
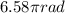 or
or
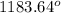
Step-by-step explanation:
Let the initial angular velocity be
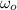 and the angular deceleration be
and the angular deceleration be
 . Equation (1) is the equivalent of the third equation of motion for a uniformly accelerated or decelerate linear motion for circular or angular motion, since the radius of the motion specified by the problem does not change.
. Equation (1) is the equivalent of the third equation of motion for a uniformly accelerated or decelerate linear motion for circular or angular motion, since the radius of the motion specified by the problem does not change.
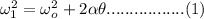
where
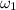 is the final angular velocity and
is the final angular velocity and
 is the angle turned through.
is the angle turned through.
Also equation (2) is a relationship between angular velocity
 and number of revolution n;
and number of revolution n;

Substituting equation (2) into (1) we obtain the following;

In the problem, our first mission is find the value of
 . When Mary spins the wheel with an initial angular velocity of 3.8rad/s, it comes to rest after making 5.5 revolutions. Therefore;
. When Mary spins the wheel with an initial angular velocity of 3.8rad/s, it comes to rest after making 5.5 revolutions. Therefore;
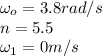
It should be noted that the wheel comes to rest that is why the final angular velocity

The angular acceleration is obtained by making
 the subject of formula from equation (3)
the subject of formula from equation (3)
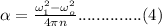
hence;
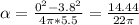
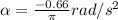
The negative result is an indication that the wheel is actually decelerating.
We then use equation (1) to determine the angle turned through when its angular velocity is 2.4rad/s as follows by making
 the subject of formula.
the subject of formula.
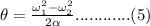
In this case,

Therefore;