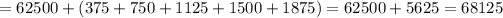The money in bank after 4 years will be
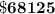
Solution:
Given, Sam deposits 12,500 each year into a retirement account with a
 simple interest rate.
simple interest rate.
He deposits the same amount each year, we have to find the amount of money will he have at the end of his fourth year.
We know that,

So, now let us find S.I after
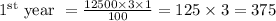
Then, after
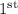 year he adds 12,500 again, which means amount doubles
year he adds 12,500 again, which means amount doubles
 S.I also doubles as rate and time of 1 year gap are constant.
S.I also doubles as rate and time of 1 year gap are constant.
Then, S.I for

Amount and corresponding S.I for 4 years will be,

Now, total balance = amount after
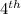 year + sum all simple interests made up to now.
year + sum all simple interests made up to now.
Total balance