Question

A farmer decides to enclose a rectangular garden using the side of the barn as on of the sides of the rectangle. what is the maximum area that the farmer can enclose with 48ft

of fence? what should the dimensions of the garden be to give this area?

Answer 1

Explanation:

Let the length of the fence = x

Let the width of the fence = y

Recall that the perimeter of a rectangle is calculated by 2(L+B) , but the farmer is using the side of the barn on one side of the rectangle , so the perimeter equation is

x + 2y = 48

Area = xy

If we substitute the perimeter equation so that the area is only in terms of y.

Area = (48 - 2y)y

Area = 48y - 2
`y^(2)`

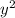
Now just find the vertex of the parabola

Area = -2
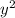`y^(2)`+ 48y

A = -2
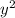`y^(2)` + 48

Differentiate A with respect to y

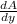`(dA)/(dy)` = -4y + 48

equate it to zero , we have

-4y + 48 = 0

4y = 48

y = 12

Substitute y = 12 into equation 1, we have

x = 48 - 2y

x = 48 - 2(12)

x = 48 - 24

x = 24

Therefore the dimensions of the garden are 24 by 12

The maximum area is 288 square unit