Question

At a certain time of day, a tree that is x meters tall casts a shadow that is x−14 meters long. If the distance from the top of the tree to the end of the shadow is x+4 meters, what is the height, x, of the tree?

At a certain time of day, a tree that is x meters tall casts a shadow that is x−14 meters long. If the distance from the top of the tree to the end of the shadow is x+4 meters, what is the height, x, of the tree?

Answer 1

Answer: 30 meters

Explanation:

This is the application of Pythagoras theorem,

the hypotenuse here is (x+4)

Applying the theorem , we have

`(x+4)^(2)` =
`x^(2)` +
`(x-14)^(2)`

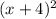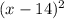
expanding , we have

`x^(2)` + 8x + 16 =
`x^(2)` +
`x^(2)` - 28x + 196

`x^(2)` + 8x + 16 = 2
`x^(2)` - 28x + 196

re arranging the equation , we have

2
`x^(2)` -
`x^(2)` - 28x - 8x + 196 - 16 = 0

`x^(2)` - 36x + 180 = 0

factorizing the quadratic equation , we have

(x-30)(x-6) = 0

Therefore , x = 30 or x = 6

With the statement , since x -14 is the shadow , which can not be negative , so x = 30