Question

An ice skater is preparing for a jump with turns and has his arms extended. His moment of inertia is 1.7 kg · m2 while his arms are extended, and he is spinning at 0.7 rev/s. If he launches himself into the air at 8.8 m/s at an angle of 45° with respect to the ice, how many revolutions can he execute while airborne if his moment of inertia in the air is 0.7 kg · m2?

Answer 1

2 revolutions.

Step-by-step explanation:

We need to obtain the angular velocity when he is in the air.

The angular momentum is given by:

`L_1=I_1*\omega_1\\L_1=1.7kg.m^2*0.7rev/s*(2\pi rad)/(1rev)=7.5kg.m^2/s`

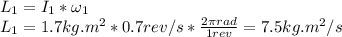
Because of angular momentum conservation L1=L2, so the final angular velocity is given by:

`\omega_2=(L1)/(I_2)=(7.5kg.m^2/s)/(0.7kg.m^2)=10.7rad/s`

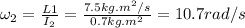
We need to calculate the time the skater is in the air, so we need to use the formula of parabolic motion:

`y=y_o+v_y*t-(1)/(2)*g*t^2\\0=0+8.8m/s*sin(45^o)*t-4.9m/s^2*t^2\\0=6.22t-4.9t^2\\solving:\\t=1.26s\\t=0`

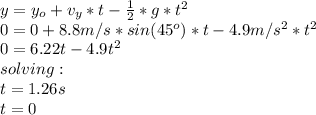
so the time taken is 1.26s

the angular displacement is given by:

`\theta=\omega*t\\\theta=13.5rad`

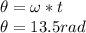
the number of revolutions is given by:

`rev=(\theta)/(2\pi)=(13.5)/(2\pi)=2.1rev`

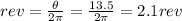
the skater execute two complete revolutions in the air.