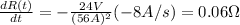Question

Electrical systems are governed by Ohm’s law, which states that V = IR, where V is the voltage, I is the current, and R is the resistance. If the current in an electrical system is decreasing at a rate of 8 amps per second while the voltage remains constant at 24 volts, at what rate is the resistance increasing (in ohms per second) when the current is 56 amps?

Answer 1

`(dR(t))/(dt)=0.06\Omega`

Step-by-step explanation:

Since
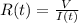`R(t)=(V)/(I(t))`, we calculate the resistance rate by deriving this formula with respect to time:

`(dR(t))/(dt)=(d)/(dt)((V)/(I(t)))=V(d)/(dt)((1)/(I(t)))`

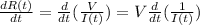
Deriving what is left (remember that
`((1)/(f(x)))'=-(1)/(f(x)^2)f'(x)`):

`(d)/(dt)((1)/(I(t)))=-(1)/(I(t)^2)(dI(t))/(dt)`

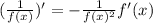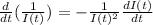
So we have:

`(dR(t))/(dt)=-(V)/(I(t)^2)(dI(t))/(dt)`

Which for our values is (the rate of I(t) is decreasing so we put a negative sign):

`(dR(t))/(dt)=-(24V)/((56A)^2)(-8A/s)=0.06\Omega`