Question

Which expressions are equal to a real number?

Answer 1

Option B

Option C

Explanation:

`$ i = √(-1) $`

⇒
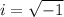
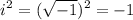`$ i^2 = (√(-1))^2 = -1 $`, which is a real number.

Similarly,
`$ i^3 = i^2.i = -1 * i = -i $`

And we also know that
`$ i^4 = 1 $`

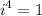
So, we see that odd powers of
`$ i $` is a complex number and even powers renders us a real number.

Using this we solve the problem.

Option A:
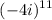`$ (-4i)^(11) $` 11 is an odd power. This would be a complex number and not a real number.

Option B:
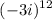`$ (-3i)^(12) $` Even power of i. So, this should give us a real number.

Option C:
`$ (2 + 3i)^2 $`

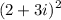
(a + bi)² = a² - b² + 2abi

So, (2 + 3i)² would be a complex number because of the 2bi term.

Option D: (4 + 5i)(4 - 5i)

(a + ib)(a - ib) = a² + b²

So, (4 + 5i)(4 - 5i) = 4² + 5² = 41, a real number.

Option E: (6 + 8i)(8 + 6i)

(a + ib)(c + id) = ac - bd + (ad + bc)i

This would be a complex number because of the (ad + bc) term.

So, Options B and D are real numbers.