Answer:
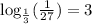
Explanation:
The given equation is

We need to write the equation in logarithmic form.
Taking log on both sides.
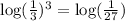
Using the property of logarithm we get
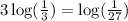
![[\because \log a^b=b\log a]](https://img.qammunity.org/2020/formulas/mathematics/high-school/gwntmx8ay9spc9lhdgck660xfa37ykhctm.png)
Divide both sides by
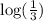 .
.
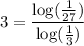
Using the property of logarithm we get

![[\because \log_x y =(\log_ay)/(\log_ax)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/atx2jysql6wsmhr0v596861r8ylqzzhmbs.png)
Therefore, the logarithmic form of given equation is
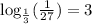 .
.