What is the ratio of the volumes of a cylinder and a cone having the same base radius and height

Question

asked Aug 9, 2020 112k views

1 Answer

Anstaendig · Answer 1 · 2020-08-15T15:05:00+0000

The ratio of the volumes of a cylinder and a cone having the same base radius and height is 3 : 1

Solution:

Given that, we have to find What is the ratio of the volumes of a cylinder and a cone having the same base radius and height.

Let "r" be the radius and "h" be the height of cylinder and cone

Let us calculate the volume of cylinder and cone

The volume of cylinder is given as:

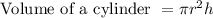
$\text { Volume of a cylinder }=\pi r^(2) h$

where "r" is the radius and "h" is the height of cylinder

The volume of cone is given as:

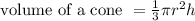
$\text { volume of a cone }=(1)/(3) \pi r^(2) h$

Now, ratio of volumes = volume of cylinder : volume of cone

$\text { Ratio of volumes }=\pi r^(2) h: (1)/(3) \pi r^(2) h$

Cancelling the common terms on both sides, we get,

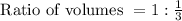
$\text { Ratio of volumes }=1: (1)/(3)$

By multiplying with 3, we get

Ratio of volumes = 3 : 1

Hence the ratio of volume of cylinder to cone is 3 : 1