Question

The mean hourly wage for employees in goods-producing industries is currently $24.57 (Bureau of Labor Statistics website, April, 1 2, 201 2). Suppose we take a sample of employees from the manufacturing industry to see if the mean hourly wage differs from the reported mean of $24.57 for the goods-producing industries.

a. State the null and alternative hypotheses we should use to test whether the population mean hourly wage in the manufacturing industry differs from the population mean hourly wage in the goods-producing industries.
b. Suppose a sample of 30 employees from the manufacturing industry showed a sam- ple mean of $23.89 per hour. Assume a population standard deviation of $2.40 per hour and compute the p-value.
c. With a = .05 as the level of significance, what is your conclusion? d. Repeat the preceding hypothesis test using the critical value approach.

Answer 1

A: 4

B:3.25

C:0.75

i didnt understand what the other guy was sayin so just in case u didnt either there u go :)

Explanation:

Answer 2

a.
`H_(0):` μ = $24.57

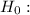`H_(a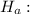):` μ ≠ $24.57

b. 0.12

c. we fail to reject the null hypothesis since p ≈0.12 > 0.05

d. we fail to reject the null hypothesis since z ≈-1.6 > -1.96

Explanation:

a)

`H_(0):` μ = $24.57

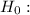`H_(a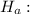):` μ ≠ $24.57

b)

To compute p value, we need to calculate z-score of $23.89 per hour. in the distribution assumed under null hypothesis

z-score can be calculated as follows:

`(X-M)/((s)/(√(N) ) )` where

• X= $23.89
• M is the mean value under null hypothesis ( $24.57)
• s is the sample standard deviation ($2.40)
• N is the sample size (30)

Putting the numbers in the formula we get

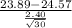`(23.89-24.57)/((2.40)/(√(30) ) )` ≈ −1,5518

The corresponding p-value is two tailed and ≈ 0.12

c)

since p ≈0.12 > 0.05 we fail to reject the null hypothesis.

d)

Critical value for the 0.05 significance level in two tailed test is :

c(z)=-1.96 Since z≈ −1,6 >-1.96, it is not in the critcal region, therefore we fail to reject the null hypothesis.