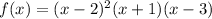Answer:
The correct answer is
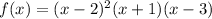
Explanation:
Every polynomial function can be factored based on its roots, then expressed in factored form.
The roots of a polynomial are the values of the variable for which the polynomial function takes the value of zero. The roots of a polynomial can be real or complex. In the graph of the polynomial function, the real roots are identified as the intersections with the x-axis (those values in which the function is zero). A polynomial function of degree "n" will have at most n roots.
Then
Polynomial function:
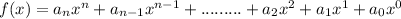
Factorized function:
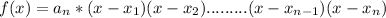
where
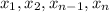 are the roots of the polynomial function.
are the roots of the polynomial function.
On the other hand, the number of times that the root repeats itself is called the multiplicity order of a root. If the order of multiplicity of the root is PAR, the graph of the function touches the
x axis but does not traverse it, REBOUNDS. If the order of multiplicity of the root is ODD, the graph of the function crosses the x axis, SHORT.
The multiplicity is expressed as an exponent in each root, as shown in the example below, where k represents the multiplicity:
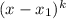
In this case, when looking at the graph, you can see that there are 3 roots in: -1, 2 and 3.
As you can also see in the graph, at -1 and 3 the root crosses the "x" axis. This indicates that the multiplicity is odd. On the other hand, in 2 the root bounces (does not cross the x axis), indicating that the multiplicity is par.
Then, the correct answer is