What are the domain and range of f(x) = (one-sixth) Superscript x + 2? domain: Left-brace x vertical-line x greater-than negative one-sixth right-brace; range: y > 0 domain:…

Question

What are the domain and range of f(x) = (one-sixth) Superscript x + 2? domain: Left-brace x vertical-line x greater-than negative one-sixth right-brace; range: y domain: Left-brace x vertical-line x greater-than one-sixth right-brace; range: y > 2 domain: x is a real number; range: y > 2 domain: x is a real number; range: y

Answer 1

C

Explanation:

domain: x ; range: y > 2

Answer 2

Option C.

Explanation:

The given function is

`f(x)=((1)/(6))^x+2`

We need to find the domain and range of the function.

Domain is the set of input values.

The given function is an exponential function. This exponential function is defined for all real values of x. So,

Domain : x is a real number

Range is the set of output values.

We know that
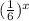`((1)/(6))^x` is always greater than 0.

`((1)/(6))^x>0`

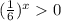
Add 2 on both sides.

`((1)/(6))^x+2>0+2`

`f(x)>2`

`y>2`

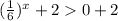
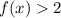
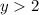
So, the rage of the function is

Range: y

Therefore, the correct option is C.