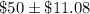Question

A major department store chain is interested in estimating the mean amount its credit card customers spent on their first visit to the chain's new store in the mall. Fifteen credit card accounts were randomly sampled and analyzed with the following results: = $50.50 and S = 20. Construct a 95% confidence interval for the mean amount its credit card customers spent on their first visit to the chain's new store in the mall assuming that the amount spent follows a normal distribution. A) $50.50 ± $9.09 B) $50.50 ± $10.12 C) $50.50 ± $11.00 D) $50.50 ± $11.08

Answer 1

Answer: D)
`\$50\pm\$11.08`

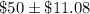
Explanation:

As per given , we have

Sample size : n= 15

sample mean :
`\overline{x}=\$50.50`

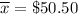
Sample standard deviation: s= $20

Since population standard deviation is unknown , so we use t-test.

Significance level for 95% confidence :
`\alpha=1-0.95=0.05`

Critical t-value :
`t_(n-1, \alpha/2)=t_(014,0.025)=2.145` [Using students' t-value table]

Required 95% Confidence interval :-

`\overline{x}\pm t_(n-1, \alpha/2)(s)/(√(n))\\\\ =\$50.50\pm(2.145)(\$20)/(√(15))\\\\\approx \$50\pm\$11.08`

Hence, the required 95% confidence interval for the mean amount its credit card customers spent on their first visit to the chain's new store in the mall assuming that the amount spent follows a normal distribution.:

`\$50\pm\$11.08`