Answer:
The speed of jogger in uphills is 4 mile per hour
And The speed of jogger in downhills is 10 mile per hour
Explanation:
Given as :
The distance cover by jogger in downhill (Dd) = 5 miles
The distance cover by jogger in uphill (Du) = 2 miles
The time taken by jogger in downhill (Td) = T hour
The time taken by jogger in uphill (Tu) = T hour
Let The speed of jogger in uphills (Su) = x mph
So ,The speed of jogger in downhills (Sd) =( x + 6 ) mph
∵, Time =
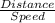
So, Tu =
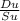
Or, T =
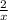 h
h
And Td =
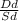
Or, T =
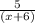 h
h
∵ Time duration of both is same
∴
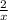 =
=
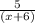
Or, 2 × (x + 6) = 5x
Or, 2x + 12 = 5x
So, 12 = 3x
∴ x =
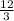 = 4 mph
= 4 mph
And x + 6 = 4 + 6 = 10 mph
Hence The speed of jogger in uphills is 4 mile per hour
And The speed of jogger in downhills is 10 mile per hour Answer