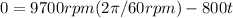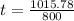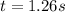A centrifuge rotor rotating at 9700 rpm is shut off and is eventually brought uniformly to rest by a frictional torque of 1.96 m⋅N . Part A If the mass of the rotor is 4.00 kg a…

Question

asked Jul 19, 2020 117k views

1 Answer

Shay Erlichmen · Answer 1 · 2020-07-24T18:31:54+0000

We start from the definition of Torque,

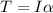
$T = I \alpha$

Where ,

I = moment of inertia

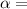$\alpha =$ Angular acceleration.

The torque given in the problem is 1.96mN.

We look for the moment of inertia of a solid cylinder,

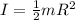
$I = \frac {1} {2} mR ^ 2$

Where m is the mass of 4Kg and R the radius 0.035m

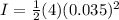
$I = \frac {1} {2} (4) (0.035) ^ 2$

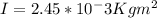
I = 2.45 * 10 ^ - 3 Kgm ^ 2

Replacing,

$-1.96 = 2.45 * 10 ^(-3) \alpha \\\alpha = -800rad / s ^ 2$

A) With angular acceleration we can find the number of revolutions, the given equation would be,

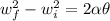
$w_f ^ 2-w_i ^ 2 = 2 \alpha \theta$

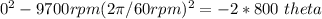
$0 ^ 2- 9700rpm (2 \pi / 60rpm) ^ 2 = -2 * 800 \ theta$

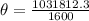
$\theta = \frac {1031812.3} {1600}$

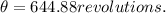
$\theta = 644.88 revolutions.$

B) We apply the rotational dynamics formula and we can find the time,

$w_f = w_i + \alpha t$

$0 = 9700 rpm (2 \pi / 60 rpm) -800t$

$t = \frac {1015.78} {800}$

t = 1.26s