Answer:
a)
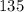 Nm⁻¹
Nm⁻¹
b)
 Hz
Hz
c)
 ms⁻¹
ms⁻¹
d)
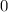 m
m
e)
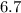 ms⁻²
ms⁻²
f)
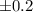 m
m
Step-by-step explanation:
a)
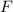 = force required to hold the object at rest connected with stretched spring = 27 N
= force required to hold the object at rest connected with stretched spring = 27 N
 = stretch in the spring from equilibrium position = 0.2 m
= stretch in the spring from equilibrium position = 0.2 m
 = force constant of the spring
= force constant of the spring
force required to hold the object at rest is same as the spring force , hence

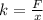
inserting the values
 Nm⁻¹
Nm⁻¹
b)
frequency of the oscillations is given as
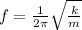
inserting the values
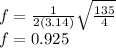 Hz
Hz
c)
 = Amplitude of oscillations = 0.2 m
= Amplitude of oscillations = 0.2 m
 = angular frequency
= angular frequency
Angular frequency is given as
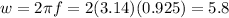 rads⁻¹
rads⁻¹
Maximum speed of oscillation is given as
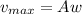
 ms⁻¹
ms⁻¹
d)
maximum speed of the object occurs at the equilibrium position, hence
 m
m
e)
Maximum acceleration of oscillation is given as
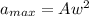
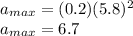 ms⁻²
ms⁻²
f)
maximum acceleration occurs when the object is at extreme positions, hence
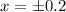 m
m