Answer:
a. W = 51,194.54 kJ
b. W = 102,390 kJ
c. W = 153,585 kJ
Step-by-step explanation:
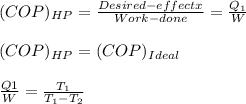
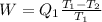
a. the ground at 15°C.
 =20°C = 273 K + 20 = 293 K
=20°C = 273 K + 20 = 293 K
 =15°C = 273 K + 15 = 288 K
=15°C = 273 K + 15 = 288 K
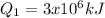


W = 51,194.54 kJ
b. a pond at 10°C.
 =10°C = 273 K + 10 = 283 K
=10°C = 273 K + 10 = 283 K

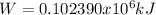
W = 102,390 kJ
c. the outside air at 5°C.
 =5°C = 273 K + 5 = 278 K
=5°C = 273 K + 5 = 278 K

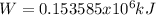
W = 153,585 kJ
Hope this helps!