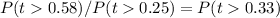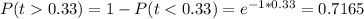Question

California is hit every year by approximately 500 earthquakes that are large enough to be felt. However, those of destructive magnitude occur, on average, once a year. Find a) Probability that at least 3 months elapse before the first earthquake of destructive magnitude occurs. b) Probability that at least 7 months elapsed before the first earthquake of destructive magnitude occurs knowing that 3 months have already elapsed.

Expert Answer

Answer 1

a) The probability that at least 3 months elapse before the first earthquake of destructive magnitude occurs is P=0.7788

b) The probability that at least 7 months elapsed before the first earthquake of destructive magnitude occurs knowing that 3 months have already elapsed is P=0.7165

Explanation:

Tha most appropiate distribution to model the probability of this events is the exponential distribution.

The cumulative distribution function of the exponential distribution is given by:

`P(t<x;\lambda)=1-e^(-\lambda t)`

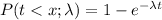
The destructive earthquakes happen in average once a year. This can be expressed by the parameter λ=1/year.

We can express the probability of having a 3 month period (t=3/12=0.25) without destructive earthquakes as:

`P(t>0.25)=1-P(t<0.25)=1-(1-e^(-1*0.25))=e^(-1*0.25)=0.7788`

Applying the memory-less property of the exponential distribution, in which the past events don't affect the future probabilities, the probability of having at least 7 months (t=0.58) elapsed before the first earthquake given that 3 months have already elapsed, is the same as the probability of having 4 months elapsed before an earthquake.

`P(t>0.58)/P(t>0.25)=P(t>0.33)`

`P(t>0.33)=1-P(t<0.33)=e^(-1*0.33)=0.7165`