Question

Find the values of x and y

Answer 1

`x=90\° \ and\ y=43\°`

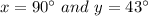
Explanation:

Given:

In
`\triangle ABC`:

`\angle ACD=47\°`

`AB\cong AC`

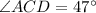
Thus the given triangle
`\triangle ABC` is an isosceles triangle as two of its sides
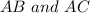`AB\ and\ AC` are congruent.

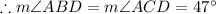`\therefore m\angle ABD=m\angle ACD=47\°` [Base angles of an isosceles triangle are congruent]

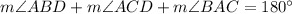`m\angle ABD+m\angle ACD+m\angle BAC=180\°` [Angle sum of a triangle =180°]

`m\angle BAC=180-(47+47)=86\°`

For an isosceles triangle the line that passes through the vertex and meets the base of the triangle is the angle bisector of the angle it passes through and also the perpendicular bisector of base.

As line
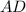`AD` passes from vertex to the base of the triangle, so we can say that line
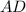`AD` is angle bisector of
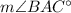`m\angle BAC\°` and perpendicular bisector of line
`BC`.

`\therefore m\angle BAD=m\angle CAD=(m\angle BAC)/(2)=(86)/(2)=43\°`

`m\angle BAD=y\°=43\°`

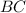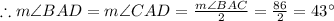
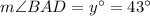
and

`AD\perp BC`

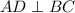
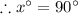`\therefore x\°=90\°` [Definition of perpendicular lines]