Answer:
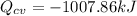
Step-by-step explanation:
Our values are,
State 1

We know moreover for the tables A-15 that
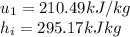
State 2

For tables we know at T=320K
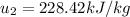
We need to use the ideal gas equation to estimate the mass, so
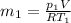
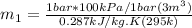
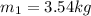
Using now for the final mass:

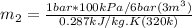
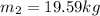
We only need to apply a energy balance equation:
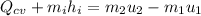
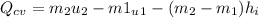
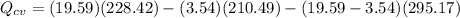
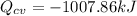
The negative value indidicates heat ransfer from the system