Answer:
25 is 2.5 standard deviations from the mean.
Explanation:
Normal probability distribution
Problems of normally distributed samples can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean.
In this question:
Mean of 15 and a standard deviation of 4, so
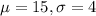
How many standard deviations from the mean is 25?
We have to find Z when
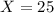 . So
. So

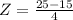
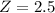
So 25 is 2.5 standard deviations from the mean.