Question

Solve through substitution

–3x+3y=4


y=x+3


Can you please give me point of intersection

Answer 1

–3x + 3y - 4 =0 and - x + y -3 = 0 do not have any solution which means two lines are parallel and there will be no intersection point.

Solution:

Need to determine solution of following system of equations

–3x + 3y = 4

y = x + 3

Let's modify given equation in standard form

–3x + 3y - 4 =0 ------- (1)

- x + y -3 = 0 ------- (2)

Lets first analyze whether given system of equation is having solution or not.

If
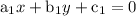`\mathrm{a}_(1) x+\mathrm{b}_(1) y+\mathrm{c}_(1)=0` and
`\mathrm{a}_(2) x+\mathrm{b}_(2) y+\mathrm{c}_(2)=0` are two equation, then if,
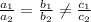`(a_(1))/(a_(2))=(b_(1))/(b_(2)) \\eq (c_(1))/(c_(2))` then the given system of equation has no solution.

In this problem,

`\begin{array}{l}{a_(1)=-3, b_(1)=3 \text { and } c_(1)=-4} \\\\ {a_(2)=-1, b_(2)=1 \text { and } c_(2)=-3} \\\\ {(a_(1))/(a_(2))=(-3)/(-1)=3} \\\\ {(b_(1))/(b_(2))=(3)/(1)=3} \\\\ {(c_(1))/(c_(2))=(-4)/(-3)=(4)/(3)}\end{array}`

`\text { In our case also } (a_(1))/(a_(2))=(b_(1))/(b_(2)) \\eq (c_(1))/(c_(2))`

So equations –3x + 3y - 4 =0 and - x + y -3 = 0 do not have any solution which means two lines are parallel and there will be no intersection point.