Question

Need help as soon as possible

Answer 1

If you solve by substitution then the answer for the first one would be (−7,−7) or x=−7,y=−7 and the second has no solution

Explanation:

Solve for the first variable in one of the equations, then substitute the result into the other equation.

Please tell me if this is right

Answer 2

System 1: x = -7; y = -7

System 2: No solution

Explanation:

We can solve both system of equations by the method of elimination.

System 1

`\begin{array}{lrcrl}(1)&-8x + 5y & = & 21 &\\(2)& -x + y & = & 0 &\\(3)&-5x + 5y &=&0&\text{Multiplied (2) by 5}\\(4)&3x & = & -21 & \text{Subtracted (1) from (3)}\\(5)&x & = &\mathbf{-7} & \text{Divided (4) by 3}\\(6)& 7+ y & = & 0 &\text{Substituted (5) into (2)}\\&y & = & \mathbf{-7} &\text{Subtracted 7 from each side}\\\end{array}`

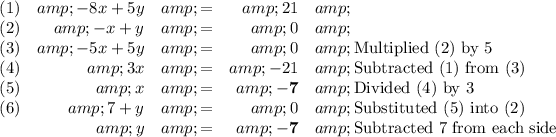
The solution is x = -7, y = -7.

System 2

`\begin{array}{lrcrl}(1)&7x + y & = & -6 &\\(2)& -21x - 3y & = & 4 &\\(3)&21x +3y &=&-18&\text{Multiplied (1) by 3}\\(4)&0 & = & -14& \text{Added (2) and(3)}\\\end{array}`

This is IMPOSSIBLE. There is NO SOLUTION.

You can write the two equations as

(1) 7x + y = -6

(2) 7x + y = -⁴/₃

The system consists of two parallel lines.