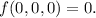Question

The function ​f(x,y,z)equals=(xyz )Superscript 1 divided by 2(xyz)1/2 has an absolute maximum value and absolute minimum value subject to the constraint xplus+yplus+zequals=11 with xgreater than or equals≥​0, ygreater than or equals≥​0, and zgreater than or equals≥0. Use Lagrange multipliers to find these values.

Answer 1

Maximum attained at point
`\left((11)/(3),(11)/(3),(11)/(3)\right).`

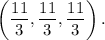
Minimum attained at point
`(0,0,0)`

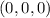
Explanation:

Write f(x,y,z) as

`f(x,y,z)=(xyz)/(2(xyz)^(1/2))=(√(xyz))/(2),`

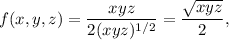
and let

`g(x)=x+y+z-11.`

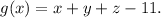
We have to optimize the function f(x,y,z) subject to g(x,y,z)=0. Using Lagrange multipliers, we have to solve the system of equations below:

`\\abla f(x,y,z)=\lambda \\abla g(x,y,z),`

`g(x,y,z)=0.`

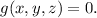
Or equivalently:

`f_x=\lambda g_x,`

`f_y=\lambda g_y,`

`f_z=\lambda g_z,`

`x+y+z=11.`

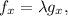
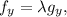
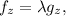
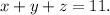
Now we calculate the partial derivatives of f and g:

`f_x=(yz)/(4√(xyz)),\ \ f_y=(xz)/(4√(xyz)),\ \ f_x=(xy)/(4√(xyz)).`

`g_x=g_y=g_z=1.`

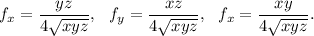
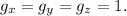
Then we have to solve the system of equations

`\begin{cases}\hfil (yz)/(4√(xyz))=\lambda & (1) \\ \hfil (xz)/(4√(xyz))=\lambda & (2) \\ \hfil (xy)/(4√(xyz)) =\lambda & (3) \\ x+y+z=1 & (4) \end{cases}`

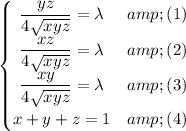
From equation (1) and (2) we get by cancelling the common factor
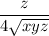`(z)/(4√(xyz))` that x = y.

Similarly, using (2) and (3) we get that y = z. Therefore, we have that x = y = z, and by equation (4), we obtain that

`x+y+z=3x=11 \Longrightarrow x=(11)/(3)`

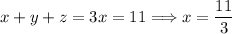
Since the function f(x,y,z) is non-negative, then
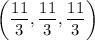`\left((11)/(3),(11)/(3),(11)/(3)\right)` is a point where f attains an absolute maximum, and

`f\left((11)/(3),(11)/(3),(11)/(3)\right)=(11√(33))/(8)\approx 3.51`

Because of the non-negativity of the function, we see that at
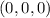`(0,0,0)` f attains an absolute minimum, and its value is

`f(0,0,0)=0.`