Question

Write the linear inequality shown in the graph.

Answer 1

`\displaystyle 4 - 3x ≥ y`

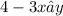
Step-by-step explanation:

Starting from the y-intercept of
`\displaystyle [0, 4],`you do
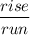`\displaystyle (rise)/(run)`by either moving three blocks north over one block west or three blocks south over one block east [west and south are negatives]. Next, we have to determine the types of inequality symbols that are suitable for this graph, which will be less than or equal to and greater than or equal to since this is a solid line graph. We then use the zero-interval test [test point (0, 0)] to ensure whether we shade the opposite portion [portion that does not contain the origin] or the portion that DOES contain the origin. At this step, we must verify the inequalities as false or true:

Greater than or equal to

`\displaystyle 0 ≥ -3[0] + 4 → 0 ≱ 4`

Less than or equal to

`\displaystyle 0 ≤ -3[0] + 4 → 0 ≤ 4`☑

This graph is shaded in the portion of the origin, so you would choose the less than or equal to inequality symbol to get this inequality:

`\displaystyle y ≤ -3x + 4`

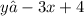
** The above answer is written in reverse, which is the exact same result.

I am joyous to assist you anytime.

Answer 2

y ≤ (4 - 3x)

Explanation:

We have to find the equation of the line which divides the coordinate plane into two different zones.

The line passes through the points (0,4) and (1,1) which is shown on the graph.

So, the equation of the straight line will be

`(y-4)/(4-1) =(x-0)/(0-1)`

⇒
`(y)/(3) - (4)/(3) =-x`

⇒ y - 4 = -3x

⇒ y = 4 - 3x

Now, the dotted zone shows that y values are equal or less than the value obtained from (4 - 3x).

Therefore, the required inequality is y ≤ (4 - 3x) (Answer)