Question

The height of a triangle is 6 centimeters less than the base. The area of the triangle is 123.5 square centimeters. Find the length of the base and the height of the triangle.

Answer 1

The length of base=19cm

The length of height=13cm

Given:

Area of the triangle A=123.5
`\mathrm{cm}^(2)`

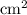
Height of the triangle h=b-6

To find:

Length of the base

Length of the height

Step by Step Explanation:

Solution:

According to the formula, Area of the triangle

`\mathrm{A}=(1)/(2) b * h`

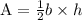
Where b=Base of the triangle

h=Height of the triangle

We know the value of A=123.5
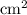`\mathrm{cm}^(2)` and also we know

h=b-6

Substitute these values in the above equation we get

123.5=
`(1)/(2) b *(b-6)`

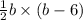
247=
`b^(2)-6 b`

`b^(2)-6 b-247=0`

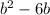
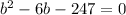
The above equation is of the form

`A x^(2)+B x+C=0`

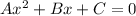
Compare the above two equations we get

A=1, B=-6, C=-247

`\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

`\frac{-(-6) \pm \sqrt{(-6)^(2)-4(1)(-247)}}{2(1)}`

`(6 \pm √(36+4(247)))/(2)`

`(6 \pm √(36+988))/(2)`

`(6 \pm √(1024))/(2)`

`(6 \pm 32)/(2 a)`

`(6+32)/(2)OR(6-32)/(2)`

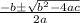
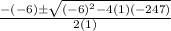
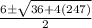
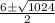
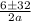
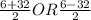
38/2 OR -26/2

The value of b can't be negative so we take

b=38/2=19cm

Though we know that

h=b-6=19-6=13cm

Result:

Thus the length values of b and h are 19 and 13 cm respectively