Question

A company estimates that the revenue​ (in dollars) from the sale of x doghouses is given by ​R(x) = 10,000 ln (0.01 x + 1). Use the differential to approximate the change in revenue from the sale of one more doghouse if 120 doghouses have already been sold.

Answer 1

$45.45

Explanation:

Data provided in the question:

Revenue function, R(x) = 10,000 ln(0.01 x + 1)

now,

change in revenue from sales doghouses i.e,
`\frac{d\textup{R}}{d\textup{x}}`

`\frac{d\textup{R}}{d\textup{x}}` =
`10,000*\frac{\textup{1}}{\textup{0.01x + 1}}*(0.01)`

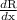
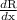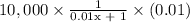
because
`\frac{d\textup{ln(A)}}{d\textup{x}}`=
`\frac{\textup{1}}{\textup{A}}*(dA)/(dx)`

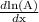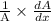
at x = 120

`\frac{d\textup{R}}{d\textup{x}}` =
`10,000*\frac{\textup{1}}{\textup{0.01(120) + 1}}*(0.01)`

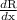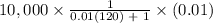
or

`\frac{d\textup{R}}{d\textup{x}}` =
`10,000*\frac{\textup{1}}{\textup{1.2 + 1}}*(0.01)`

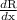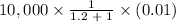
or

`\frac{d\textup{R}}{d\textup{x}}` =
`10,000*\frac{\textup{1}}{\textup{2.2}}*(0.01)`

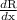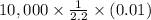
or

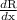`\frac{d\textup{R}}{d\textup{x}}` = $45.45

hence,

the change in revenue from the sale of one more doghouse if 120 doghouses have already been sold is $45.45