Question

State the domain and end behavior of each rational function. Identify all horizontal and vertical asymptotes on the

graph of each rational function. Then, verify your answer by graphing the function on the graphing calculator.
1. f(x) = −x + 6 / 2x + 3
2. f(x) = 3x − 6 / x
3. f(x) = 3 / x2 − 25
4. f(x) = x2 − 2 / x2 + 2x − 3
5. f(x) = x2 − 5x − 4 / x + 1
6. f(x) = 5x / x2 + 9

Answer 1

Rational Functions

Explanation:

1)

`f(x) = - (x + 6)/(2x + 3)`

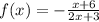
• State the domain

X ∈ R :
`x \\eq - (3)/(2)`

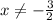
• End Behaviour

`x \rightarrow \infty , y \rightarrow -(1)/(2)`

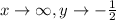
• Horizontal and Vertical

`y= -(1)/(2) , x=-(3)/(2)`

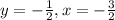
• Graphic (Annex)

2)
`f(x) =  (3x − 6)/(x)`

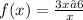
• State the domain

X ∈ R :
`x \\eq  0`

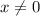
• End Behaviour

`x \rightarrow \infty , y \rightarrow 3`

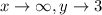
• Horizontal and Vertical

`y= 0`

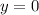
• Graphic (Annex)

3)
`f(x) =  (3)/(x^2-25)`

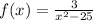
• State the domain

X ∈ R :
`x \\eq  5.5`

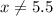
• End Behaviour

`x \rightarrow +/-\infty , y \rightarrow 0`

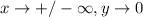
• Horizontal and Vertical

`y= 0 , x=+/- 5`

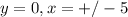
• Graphic (Annex)

4)
`f(x) = ( x^2-2)/(x^2+2x-3)`

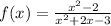
• State the domain

X ∈ R :
`x \\eq  (3,1)`

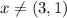
• End Behaviour

`x \rightarrow +/-\infty , y \rightarrow +/- 1`

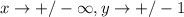
• Horizontal and Vertical

`y= 1 , x= (-3,1)`

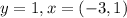
• Graphic (Annex)

5)
`f(x) =  ( x^2 − 5x − 4)/(x + 1)`

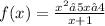
• State the domain

X ∈ R :
`x \\eq  -1`

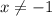
• End Behaviour

`x \rightarrow +/-\infty , y \rightarrow +/ \infty`

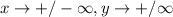
• Horizontal and Vertical

`y=none , x= -1`

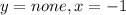
• Graphic (Annex)

6)
`f(x) = ( 5x )/(x^2 + 9 )`

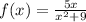
• State the domain

X ∈ R

• End Behaviour

`x \rightarrow +/-\infty , y \rightarrow 0`

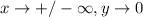
• Horizontal and Vertical

`y= 0 , x= none`

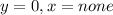
• Graphic (Annex)