Question

Taletha is preparing for an exam in Algebra II. She knows she will be expected to determine if two functions are inverses of each other using composition of functions. Which compositions would she use to prove f(x) and g(x) are inverse functions?

f ○ g(x) = and g ○ f(x) =

⊝


f ○ g(x) = x and g ○ f(x) =

⊝


f ○ g(x) = x and g ○ f(x) = x

⊝


f ○ g(x) = and g ○ f(x) = x

Answer 1

f ○ g(x) = x and g ○ f(x) = x is the correct composition

Explanation:

INVERSE FUNCTIONS: Two functions are said to be inverse of each other if for every y = f(x), there exists a function g(x),

such that x =
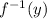`f^(-1) (y)` = g(y)

Now, here if we need to show tha two functions f(x) and g(x) are inverse functions of each other , then show that for every x:

1. f o g(x) = f(g(x))= x

2. g o f(x) = g(f(x)) = x

If any two functions satisfy these two conditions, then they are inverse of each other.