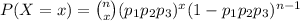Question

There are n people eligible to vote in a certain election. Voting requires registration. Decisions are made independently. Each of the n people will register with probability p1. Given that a person registers, he or she will vote with probability p2. Given that a person votes, he or she will vote for Kodos (who is one of the candidates) with probability p3. What is the distribution of the number of votes for Kodos (give the PMF fully simplified).

Answer 1

n= 3150

Explanation:

Answer 2

The probability is:

`X\sim Bin (n,p_1p_2,p_3)`

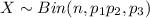
or
`P(X=x)=\binom{n}{x}(p_1p_2p_3)^x(1-p_1p_2p_3)^(n-1)`

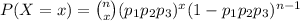
Explanation:

Consider the provided information.

Each of the n people will register with probability p1. Given that a person registers, he or she will vote with probability p2. Given that a person votes, he or she will vote for Kodos (who is one of the candidates) with probability p3.

There is only one way to vote for Kodos

That is the person should be register, and will vote in the favor of Kodos.

Hence, the probability is:

`X\sim Bin (n,p_1p_2,p_3)`

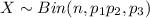
Where X is the number of votes for Kodos.

The Required PMF is:

`P(X=x)=\binom{n}{x}(p_1p_2p_3)^x(1-p_1p_2p_3)^(n-1)`