Answer:
Tangential Velocity = 30.24 m/s
Step-by-step explanation:
Given that,
Mass of ball, m = 0.04 Kg
Length of the string, r = 0.70 m
Acceleration of the ball, a = 43.2 m/s²
The tangential velocity of ball, V = ?
The centripetal force is given by the relation
Fc = mV²/r newton
where, m - mass of body
V - tangential velocity of body
r - radius of the trajectory
Force applied on the ball to rotate on a circular path
F = m x a newton
The applied force is equal to centripetal force.
So, equalizing the force equations
m x a = m V²/r
Therefore
V² = a x r
V =
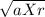
Substituting the values
V =
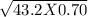
V = 30.24 m/s
So, the tangential velocity of the ball is 30.24 m/s