Question

Two distinct solid fuel propellants, type A and type B, are being considered for a space program activity. Burning rates of the propellant are crucial. Random samples of 12 specimens of propellant A are taken with sample means of 84 cm/sec with a standard deviation of 4. And, random samples of 18 specimens of propellant B are taken with sample means of 77 cm/sec with a standard deviation of 6. Find a 99% confidence interval for the difference between the average burning rates for the two propellants. Assume the populations to be approximately normally distributed with equal variances.

Answer 1

C.I. = (2.297, 11.703)

Explanation:

The t-statistic for difference of mean is given by,

`t=\frac{\bar{x_(1)}-\bar{x_(2)}}{\sqrt{(s_(1)^(2))/(n_(1))+(s_(2)^(2))/(n_(2))}}`

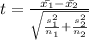
Here,
`\bar{x_(1)}` = 84

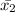`\bar{x_(2)}` = 7

s₁ = 4

n₁ = 12

s₂ = 6

n₂ = 18

Substituting all value in formula,

We get, t = -3.541 at 28 degree of freedom.

Using this formula, we get, t = 1.5342

Therefore, based on the data provided, the 99% confidence interval for the difference between the population means
`\bar{x_(1)}-\bar{x_(2)}` is: 2.297 <
`\bar{x_(1)}-\bar{x_(2)}` < 11.703

which indicates that we are 99% confident that the true difference between population means is contained by the interval (2.297, 11.703)