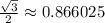Question

Find cos 0 for 0 = 30°

The 0 has a weird line through it​

Answer 1

Answer:
`(√(3))/(2)`

======================================================

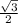
Step-by-step explanation:

The symbol
`\theta` is the greek letter theta. It's often used in trigonometry for angles.

In this case,
`\theta = 30^(\circ)`

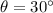
So,

`\cos(\theta) = \cos(30^(\circ)) = (√(3))/(2)`

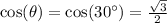
You'll need to use a reference sheet or the unit circle to determine the value of cos(30). Or you could use a 30-60-90 triangle template.

When using the unit circle, look in the upper right quadrant (which is quadrant 1). The angle 30 degrees is in this quadrant. Locate the terminal point and note how
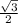`(√(3))/(2)` is the x coordinate of the terminal point. This is due to
`x = \cos(\theta)`

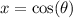
Side note:
`(√(3))/(2) \approx 0.866025`