With
 , we have by the fundamental theorem of calculus
, we have by the fundamental theorem of calculus
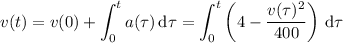
Differentiating both sides wrt
 gives
gives
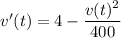
This equation is separable as
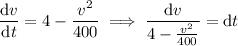
Integrate both sides; on the left, substitute

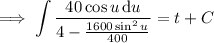
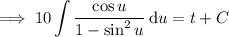

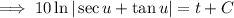

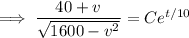
Given that
 , we have
, we have

So the velocity at time
 is
is
 that satisfies
that satisfies
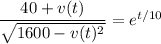
When
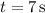 , we have
, we have
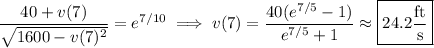
We can rewrite the particular solution as
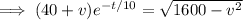
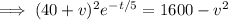
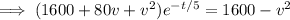
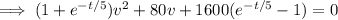
Taking the limit as
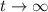 on both sides gives
on both sides gives
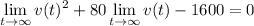
(the exponential terms approach 0)
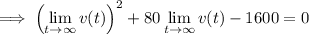
so the limiting velocity, call it
 , satisfies the quadratic equation
, satisfies the quadratic equation

Realistically, the boat won't speed up enough for the resistance to be so strong as to reverse the boat's direction, so the limiting velocity should be positive.