Due to a manufacturing error, two cans of regular soda were accidentally filled with diet soda and placed into a 18-pack. Suppose that two cans are randomly selected from the 18…

Question

asked Jan 22, 2020 54.4k views

1 Answer

Marc Witteveen · Answer 1 · 2020-01-29T00:43:37+0000

Answer:

a) There is a 1.21% probability that both contain diet soda.

b) There is a 79.21% probability that both contain diet soda.

c)
P(X = 2) is unusual,
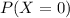P(X = 0) is not unusual

d) There is a 19.58% probability that exactly one is diet and exactly one is regular.

Explanation:

There are only two possible outcomes. Either the can has diet soda, or it hasn't. So we use the binomial probability distribution.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

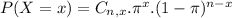
$P(X = x) = C_(n,x).\pi^(x).(1-\pi)^(n-x)$

In which
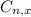C_(n,x) is the number of different combinatios of x objects from a set of n elements, given by the following formula.

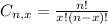
C_(n,x) = (n!)/(x!(n-x)!)

And
$\pi$ is the probability of X happening.

A number of sucesses
is considered unusually low if
$P(X \leq x) \leq 0.05$ and unusually high if
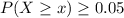
$P(X \geq x) \geq 0.05$

In this problem, we have that:

Two cans are randomly chosen, so
n = 2

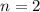
Two out of 18 cans are filled with diet coke, so
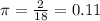
$\pi = (2)/(18) = 0.11$

a) Determine the probability that both contain diet soda. P(both diet soda)

That is P(X = 2).

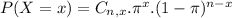
$P(X = x) = C_(n,x).\pi^(x).(1-\pi)^(n-x)$

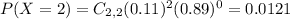
P(X = 2) = C_(2,2)(0.11)^(2)(0.89)^(0) = 0.0121

There is a 1.21% probability that both contain diet soda.

b)Determine the probability that both contain regular soda. P(both regular)

That is P(X = 0).

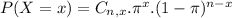
$P(X = x) = C_(n,x).\pi^(x).(1-\pi)^(n-x)$

P(X = 0) = C_(2,0)(0.11)^(0)(0.89)^(2) = 0.7921

There is a 79.21% probability that both contain diet soda.

c) Would this be unusual?

We have that
P(X = 2) is unusual, since
$P(X \geq 2) = P(X = 2) = 0.0121 \leq 0.05$

For P(X = 0), it is not unusually high nor unusually low.

d) Determine the probability that exactly one is diet and exactly one is regular. P(one diet and one regular)

That is P(X = 1).

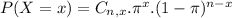
$P(X = x) = C_(n,x).\pi^(x).(1-\pi)^(n-x)$

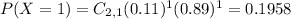
P(X = 1) = C_(2,1)(0.11)^(1)(0.89)^(1) = 0.1958

There is a 19.58% probability that exactly one is diet and exactly one is regular.