Question

"Sam is fond of taking long-distance trips. During each trip his car has a tire failure in each 100-mile stretch with a probability of 0.05. He recently embarked on an 800-mile trip and took two spare tires with him on the trip. (a) What is the probability that the first change of tire occurred 300 miles from his starting point? (b) What is the probability that his second change of tire occurred 500 miles from his starting point? (c) What is the probability that he completed the trip without having to change tires?"

Answer 1

We are given that During each trip his car has a tire failure in each 100-mile stretch with a probability of 0.05.

Probability of failure = 0.05

Probability of success = 1- 0.05 = 0.95

a) What is the probability that the first change of tire occurred 300 miles from his starting point?

So, no change in 1st 100 mile + no change in 2nd 100 mile+ change in 3rd 100 miles

So, the probability that the first change of tire occurred 300 miles from his starting point = 0.95 * 0.95 * 0.05 =0.0451

Hence the probability that the first change of tire occurred 300 miles from his starting point is 0.0451

b) What is the probability that his second change of tire occurred 500 miles from his starting point?

So, no change in 1st 400 miles + change in last 100 miles

So,the probability that his second change of tire occurred 500 miles from his starting point =
`^4C_1 * 0.05 * (0.95)^3 * 0.05`

=
`0.0514`

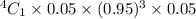
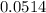
Hence the probability that his second change of tire occurred 500 miles from his starting point 0.0514

c) What is the probability that he completed the trip without having to change tires?"

No change after 800 miles

Probability that he completed the trip without having to change tires :

=
`(0.95)^8`

=
`0.6634`

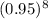
Hence the probability that he completed the trip without having to change tires is 0.6634