Question

Given the following statistics for women over the age of 50 entering our medical clinic:

(a) 1% actually have breast cancer
(b) 90% of the women who have breast cancer are going to get a positive test result (affirming that they have the disease)
(c) 8% of those that actually don’t have the disease are going to be told that they do have breast cancer (a "false positive")

What’s the actual probability, if a woman gets a positive test result, that she actually does have breast cancer?

Answer 1

P(breast cancer) = 0.01

P(no breast cancer ) = 1-0.01 = 0.99

P(positive | breast cancer)= 0.90

P(positive | no breast cancer ) = 0.08

P(breast cancer | positive ) =
`\frac{P(\text{breast cancer}) * P(\frac{positive}{\text{cancer}})}{P(\text{breast cancer}) * P(\frac{positive}{\text{cancer}}) + P(\text{ no breast cancer}) * P(\frac{positive}{\text{no cancer}})}`

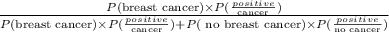
Substitute the values :

P(breast cancer | positive ) =
`(0.10 * 0.90)/(0.10 * 0.90+0.99 * 0.08)`

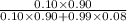
P(breast cancer | positive ) =
`0.531`

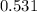
Hence the actual probability, if a woman gets a positive test result, that she actually does have breast cancer is 0.531