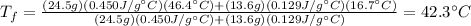Question

A sheet of gold weighing 13.6 g and at a temperature of 16.7°C is placed flat on a sheet of iron weighing 24.5 g and at a temperature of 46.4°C. What is the final temperature of the combined metals? Assume that no heat is lost to the surroundings. (Hint: The heat gained by the gold must be equal to the heat lost by the iron.)

Answer 1

`T_f=42.3^(\circ)C`

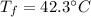
Step-by-step explanation:

The heat released by the iron is absorbed by the gold. This quantity is calculated with the formula
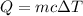`Q=mc\Delta T`, which tells us the amount of heat (energy) Q needed to increase the temperature of a material of mass m, specific heat c by a temperature difference
`\Delta T`.

Since the heat released (which we will take as negative Q) by the iron (Fe) is absorbed (positive Q then) by the gold (Au) we write
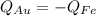`Q_(Au)=-Q_(Fe)`, which means
`m_(Au)c_(Au)\Delta T_(Au)=-m_(Fe)c_(Fe)\Delta T_(Fe)`, which is to say
`m_(Au)c_(Au)(T_(fAu)-T_(0Au))=-m_(Fe)c_(Fe)(T_(fFe)-T_(0Fe))`.

We know that thermal equilibrium has been reached, which means that at the end everything has the same temperature, so we have
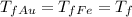`T_(fAu)=T_(fFe)=T_f`, and we can substitute
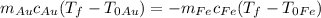`m_(Au)c_(Au)(T_f-T_(0Au))=-m_(Fe)c_(Fe)(T_f-T_(0Fe))` and do
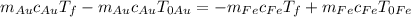`m_(Au)c_(Au)T_f-m_(Au)c_(Au)T_(0Au)=-m_(Fe)c_(Fe)T_f+m_(Fe)c_(Fe)T_(0Fe)`, to get finally
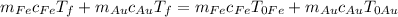`m_(Fe)c_(Fe)T_f+m_(Au)c_(Au)T_f=m_(Fe)c_(Fe)T_(0Fe)+m_(Au)c_(Au)T_(0Au)`, which means
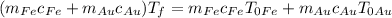`(m_(Fe)c_(Fe)+m_(Au)c_(Au))T_f=m_(Fe)c_(Fe)T_(0Fe)+m_(Au)c_(Au)T_(0Au)`, giving us the final formula
`T_f=(m_(Fe)c_(Fe)T_(0Fe)+m_(Au)c_(Au)T_(0Au))/(m_(Fe)c_(Fe)+m_(Au)c_(Au))`.

We can get from tables that
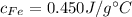`c_(Fe)=0.450J/g^(\circ)C` and
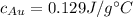`c_(Au)=0.129J/g^(\circ)C`, so we put everything in a calculator and we get
`T_f=((24.5g)(0.450J/g^(\circ)C)(46.4^(\circ)C)+(13.6g)(0.129J/g^(\circ)C)(16.7^(\circ)C))/((24.5g)(0.450J/g^(\circ)C)+(13.6g)(0.129J/g^(\circ)C))=42.3^(\circ)C`