Question

The data to the right represent the weights​ (in grams) of a random sample of 50 candies. Complete parts​ (a) through​ (f). 0.920.92 0.870.87 0.880.88 0.820.82 0.820.82 0.870.87 0.970.97 0.860.86 0.890.89 0.840.84 0.810.81 0.880.88 0.770.77 0.860.86 0.930.93 0.840.84 0.720.72 0.820.82 0.740.74 0.830.83 0.930.93 0.750.75 0.790.79 0.910.91 0.840.84 0.910.91 0.880.88 0.880.88 0.830.83 0.780.78 0.990.99 0.810.81 0.780.78 0.750.75 0.820.82 0.760.76 0.820.82 0.870.87 0.910.91 0.770.77 0.720.72 0.940.94 0.710.71 0.730.73 0.810.81 0.810.81 0.860.86 0.930.93 0.930.93 0.820.82 ​(a) Determine the sample standard deviation weight.

Answer 1

0.069

Explanation:

The given data set is

0.92, 0.87, 0.88, 0.82, 0.82, 0.87, 0.97, 0.86, 0.89, 0.84, 0.81, 0.88, 0.77, 0.86, 0.93, 0.84, 0.72, 0.82, 0.74, 0.83, 0.93, 0.75, 0.79, 0.91, 0.84, 0.91, 0.88, 0.88, 0.83, 0.78, 0.99, 0.81, 0.78, 0.75, 0.82, 0.76, 0.82, 0.87, 0.91, 0.77, 0.72, 0.94, 0.71, 0.73, 0.81, 0.81, 0.86, 0.93, 0.93, 0.82.

Formula for mean:

`Mean=(\sum x)/(n)`

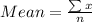
Sum of all terms = 41.98

Mean of the data set is

`Mean=(41.98)/(50)`

`Mean=0.8396`

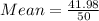
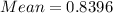
Formula for standard deviation for population:

`\sigma=\sqrt{\frac{\sum (x-\overline{x})^2}{n}}`

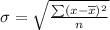
Formula for standard deviation for sample:

`\sigma=\sqrt{\frac{\sum (x-\overline{x})^2}{n-1}}`

`\sigma=\sqrt{(0.231792)/(50-1)}`

`\sigma=√(0.004730449)`

`\sigma=0.06877826`

`\sigma\approx 0.069`

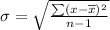
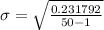
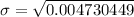
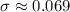
Therefore, the standard deviation of the data set is 0.069.