Question

The function f(x) = ax^4 + 8x^2 has three turning points, an absolute maximum of 8, and one of its zeros at x = 2. Determine the value of a and the location of the other zeros.

Answer 1

The value of a = -2.

The value of the zeros are -2, +2, 0.

Explanation:

Let's first calculate the value of a, knowing that there is a zero at x =2 (meaning that f(2)=0):

`f(x)=ax^(4) + 8x^(2)\\f(2)=a(2)^(4) + 8(2)^(2)=0\\16a+32=0\\16a=-32\\a=-2`

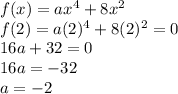
The function now looks like this:
`f(x)=-2x^(4) + 8x^(2)`

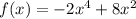
In order to find the other zeros, let's factorize:

`f(x)=-2x^(4) + 8x^(2)\\f(x)=-2*(x^(2))*(x^(2) - 4)\\f(x)=-2*(x^(2))*(x-2)*(x+2)\\`

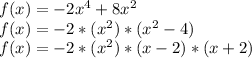
So the value of the zeros are -2, +2, 0.