Question

The Ha line of the Balmer series is emitted in the transition from n-3 to n 2. Compute the wavelength of this line for H and 2H. [Note: These are the electronic hydrogen and deuterium atoms, not the muonic forms.]

Answer 1

Step-by-step explanation:

According to Rydberg's formula, the wavelength of the balmer series is given by:

`(1)/(\lambda)=R((1)/(2^2)-(1)/(3^2))`

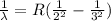
R is Rydberg constant for an especific hydrogen-like atom, we may calculate R for hydrogen and deuterium atoms from:

`R=(R_(\infty))/((1+(m_e)/(M)))`

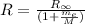
Here,
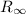`R_(\infty)` is the "general" Rydberg constant,
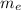`m_e` is electron's mass and M is the mass of the atom nucleus

For hydrogen, we have,
`M=1.67*10^(-27)kg`:

`R_H=(1.09737*10^7m^(-1))/((1+(9.11*10^(-31)kg)/(1.67*10^(-27)kg)))\\R_H=1.09677*10^7m^(-1)`

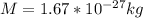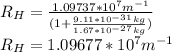
Now, we calculate the wavelength for hydrogen:

`(1)/(\lambda)=R_H((1)/(2^2)-(1)/(3^2))\\\lambda=[R_H((1)/(2^2)-(1)/(3^2))]^(-1)\\\lambda=[1.0967*10^7m^(-1)((1)/(2^2)-(1)/(3^2))]^(-1)\\\lambda=6.5646*10^(-7)m=656.46nm`

For deuterium, we have
`M=2(1.67*10^(-27)kg)`:

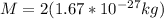`R_D=(1.09737*10^7m^(-1))/((1+(9.11*10^(-31)kg)/(2*1.67*10^(-27)kg)))\\R_D=1.09707*10^7m^(-1)\\\\\lambda=[R_D((1)/(2^2)-(1)/(3^2))]^(-1)\\\lambda=[1.09707*10^7m^(-1)((1)/(2^2)-(1)/(3^2))]^(-1)\\\lambda=6.5629*10^(-7)=656.29nm`