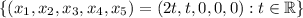Question

1. Solve the following system of equations by performing Gaussian Elimination on the corresponding augmented matrix. X1 – 2x2 + x3 + 4x4 – 25 = 0 -2x1 + 4x2 + x3 – 224 – 45 = 0 3x1 – 6x2 + 8x3 + 4x4 – 13x5 = 0) 8x1 – 16x2 + 7x3 + 12x4 – 6x 5 = 0

Answer 1

The system to solve is

`x_1-2x_2+x_3+4x_4-2x_5=0\\-2x1+4x_2+x_3-2x_4-4x_5=0\\3x_1-6x_2+8x_3+4x_4-13x_5=0\\8x_1-16x_2+7x_3+12x_4-6x_5=0`

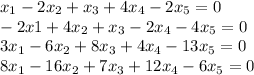
and the augmented matrix of the system is
`\left[\begin{array}{cccccc}1&-2&1&4&-2&0\\-2&4&1&-2&-4&0\\3&-6&8&4&-13&0\\8&-16&7&12&-6&0\end{array}\right]`

Using row operations we obtain the echelon form of the matrix, that is,

`\left[\begin{array}{ccccccc}1&-2&1&4&-2&0\\0&0&-1&-20&10&0\\0&0&0&-54&22&0\\0&0&0&0&13&0\end{array}\right]`

Now, we use backward substitution:

1.
`13x_5=0,\; x_5=0`

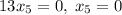
2.

`54x_4+22x_5=0\\54x_4+22*0=0\\x_4=0`

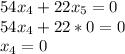
3.

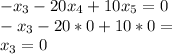
`-x_3-20x_4+10x_5=0\\-x_3-20*0+10*0=\\x_3=0`

4.

`x_1-2x_2+x_3+4x_4-2x_5=0\\x_1-2x_2+0+4*0-2*0=0\\x_1=2x_2`

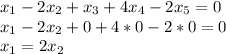
The system has infinite solutions and the set of solutions is:

`\{(x_1,x_2,x_3,x_4,x_5)=(2t,t,0,0,0): t\in\mathbb{R}\}`