Answer: The equilibrium concentration of
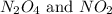 are 0.0164 M and 0.0572 M
are 0.0164 M and 0.0572 M
Step-by-step explanation:
We are given:
Initial concentration of
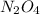 = 0.0654 M
= 0.0654 M
The given chemical equation follows:
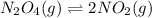
Initial: 0.0654
At eqllm: 0.0654 - x 2x
The expression of
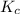 for above reaction follows:
for above reaction follows:
![K_c=([NO_2]_(eq)^2)/([N_2O_4]_(eq))](https://img.qammunity.org/2020/formulas/chemistry/college/jlmvwmrzyapor7exequj8n0c1w9fy0vkig.png)
We are given:
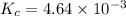
![[NO_2]_(eq)=2x](https://img.qammunity.org/2020/formulas/chemistry/college/rqkfhai1vorwlju8z09fira9lje06xros3.png)
![[N_2O_4]_(eq)=0.0654-x](https://img.qammunity.org/2020/formulas/chemistry/college/4r3u4xoyefox1s6aietqxtmuk29i5fx0x0.png)
Putting values in above equation, we get:
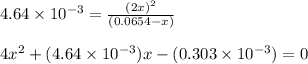
Solving for the value of 'x', we get:
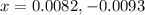
Neglecting the negative value of 'x', as concentration cannot be negative.
Now,
![[NO_2]_(eq)=2x=2(0.0082)=0.0164M](https://img.qammunity.org/2020/formulas/chemistry/college/zyqloup0b5lsmtvf2q4sl5pc1j0n20uno8.png)
![[N_2O_4]_(eq)=0.0654-x=(0.0654-0.0082)=0.0572M](https://img.qammunity.org/2020/formulas/chemistry/college/vycc6hprtn9c0vt9fhbt1shu5bqt28w8yc.png)
Hence, the equilibrium concentration of
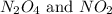 are 0.0164 M and 0.0572 M
are 0.0164 M and 0.0572 M