Question

If f(x) = 3x2 + 2 and g(x) = x2 - 9, find (f - g)(x).

O A. 2x +11
O B. 2x² - 7
O C. 4x2 +11
O D. 44²-7

Answer 1

The simplified expression for (f - g)(x) is 2x + 11. Option A is answer.

Step-by-step explanation:

To find (f - g)(x), we need to subtract the function g(x) from the function f(x). Here's how we do it:

Substitute the expressions for f(x) and g(x):

(f - g)(x) = (3x^2 + 2) - (x^2 - 9)

Distribute any negative signs:

(f - g)(x) = 3x^2 + 2 - x^2 + 9

Combine like terms:

(f - g)(x) = (3x^2 - x^2) + (2 + 9)

(f - g)(x) = 2x^2 + 11

Therefore, the simplified expression for (f - g)(x) is 2x^2 + 11.

So the correct answer is A. 2x + 11.

Answer 2

From the options given, there is no correct answer in the option.

`(f-g)(x)=2 x^(2)+11`

Given:

`f(x)=3 x^(2)+2`

`g(x)=x^(2)-9`

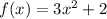
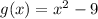
Step-by-step explanation:

From question, we need to find the subtraction of the given functions. In this step, we need to find the subtraction of the two functions. The given are functions of ‘x’.

`(f-g)(x)=f(x)-g(x)`

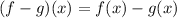
Now, we need to substitute the each functions,

`\Rightarrow(f-g)(x)=\left(3 x^(2)+2\right)-\left(x^(2)-9\right)`

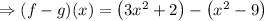
Now, we need to multiply the signs with the numbers inside the bracket,

`\Rightarrow(f-g)(x)=3 x^(2)+2-x^(2)+9`

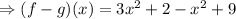
Now, on adding and subtracting,

`\therefore(f-g)(x)=2 x^(2)+11`

Thus, we found the subtraction of the given functions.