Question

Two projectiles are thrown with the same initial speed, one at an angle θ with respect to the level ground and the other at angle 90° − θ. Both projectiles strike the ground at the same distance from the projection point. Are both projectiles in the air for the same length of time?

Answer 1

Height is different for both .

The time in air are different for both.

Explanation:

Given that initial velocity is same

Lets take initial velocity = u

One at an angle θ.

other at angle 90° − θ.

Also given that their range are same

`R_1=R_2`

`R_1=(u^2sin2\theta )/(g)`

`R_2=(u^2sin2(90-\theta))/(g)`

`R_2=(u^2sin(180-2\theta))/(g)`

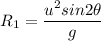
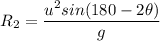
We know that

sin(180° − θ)=sin θ

So

`R_2=(u^2sin2\theta )/(g)`

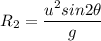
Height in the air

`h_1=(u^2sin^2\theta)/(2g)`

`h_2=(u^2sin^2(90-\theta))/(2g)`

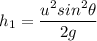
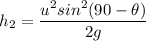
We know that

sin(90° − θ)=cos θ

`h_2=(u^2cos^2\theta)/(2g)`

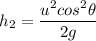
From above we can say that height is different for both .

Time:

`T_1=(2usin\theta)/(g)`

`T_2=(2usin(90-\theta))/(g)`

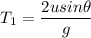
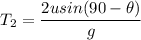
sin(90° − θ)=cos θ

`T_2=(2ucos\theta)/(g)`

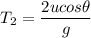
The time in air are different for both.