Question

The mean weight of an adult is 62 kilograms with a variance of 144.If 195 adults are randomly selected, what is the probability that the sample mean would differ from the population mean by greater than 2.2 kilograms? Round your answer to four decimal places.

Answer 1

The probability that the sample mean would differ from the population mean by greater than 2.2 kilograms is 0.0104 .

Explanation:

The mean weight of an adult is 62 kilograms with a variance of 144

i.e.
`\mu = 62 \\\sigma^2 = 144`

We are supposed to find probability that the sample mean would differ from the population mean by greater than 2.2 kilograms

i.e.
`P(\bar{x}<62-2.2) or P(\bar{x}>62+2.2)=1-P(59.8<\bar{x}<64.2)`

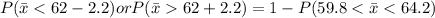
Using formula :
`(x-\mu)/((\sigma)/(√(n)))`

`P(\bar{x}<62-2.2) or P(\bar{x}>62+2.2)=1-P(59.8<\bar{x}<64.2)`

`P(\bar{x}<62-2.2) or P(\bar{x}>62+2.2)=1-P((59.8-62)/((12)/(√(195)))<(64.2-62)/((12)/(√(195))))`

`P(\bar{x}<62-2.2) or P(\bar{x}>62+2.2)=1-P(-2.56<z<2.56)`

`P(\bar{x}<62-2.2) or P(\bar{x}>62+2.2)=1-{P(z<2.56)-P(z<-2.56)}`

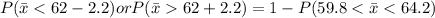
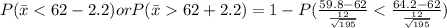
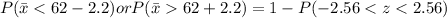
Refer the z table

`P(\bar{x}<62-2.2) or P(\bar{x}>62+2.2)=1-{0.9948-0.0052}`

`P(\bar{x}<62-2.2) or P(\bar{x}>62+2.2)=0.0104`

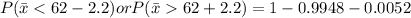
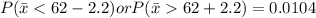
Hence The probability that the sample mean would differ from the population mean by greater than 2.2 kilograms is 0.0104 .