Answer: 1.7
Explanation:
Given : The probability that a radish seed will germinate is p=0.7.
A gardener plants seeds in batches of n=14.
For binomial distribution, the standard deviation is given by :-
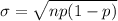
Then, the standard deviation for the number of seeds germinating in each batch will be :-
![\sigma=√(14(0.7)(1-0.7))\\\\=√(14(0.7)(0.3))\\\\=√(2.94)=1.71464281995\approx1.7\ \ [\text{Rounded to the nearest tenth}]](https://img.qammunity.org/2020/formulas/mathematics/high-school/f2fsqc6gkaxb2zi1o9o50fsmluxp4bcb3i.png)
Hence, the standard deviation for the number of seeds germinating in each batch =1.7