Question

If x and y are integers greater than 1, is x a multiple of y ? (1) \small 3y^{2}+7y=x (2) \small x^{2}-x is a multiple of y. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. EACH statement ALONE is sufficient. Statements (1) and (2) TOGETHER are NOT sufficient.

Answer 1

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.

Explanation:

A multiple of a number is obtained after multiplying the number by an integer.

Here,

x, y are any two integers greater than 1,

(1) We have,

`\small 3y^(2)+7y=x`

`\implies y(3y+7) = x`

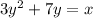
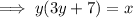
∵ y is an integer ⇒ 3y + 7 is also an integer,

⇒ y × an integer = x

That is, when we multiply y by a number we obtain x,

∴ x is a multiple of y.

Thus, statement (1) ALONE is sufficient.

(2),

`\small x^(2)-x\text{ is a multiple of y}`

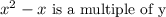
I.e.

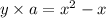`y* a = x^2-x`, where a is an integer,

`\implies y* a = x(x-1)`

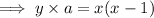
∵ x and x - 1 are disjoint numbers,

There are three possible cases,

Case 1 : x is multiple of y

Case 2 : (x-1) is a multiple of y,

Case 3 : neither x nor x - 1 are multiple of y but their product is multiple of y,

Thus, statement (2) is not sufficient.