Question

Captain John Stapp is often referred to as the "fastest man on Earth." In the late 1940s and early 1950s, Stapp ran the U.S. Air Force's Aero Med lab, pioneering research into the accelerations which humans could tolerate and the types of physiological effects which would result. After several runs with a 185-pound dummy named Oscar Eightball, Captain Stapp decided that tests should be conducted upon humans. Demonstrating his valor and commitment to the cause, Stapp volunteered to be the main subject of subsequent testing. Manning the rocket sled on the famed Gee Whiz track, Stapp tested acceleration and deceleration rates in both the forward-sitting and backward-sitting positions. He would accelerate to aircraft speeds along the 1200-foot track and abruptly decelerate under the influence of a hydraulic braking system. On one of his most intense runs, his sled decelerated from 282 m/s (632 mi/hr) to a stop at -201 m/s/s. Determine the stopping distance and the stopping time.

Answer 1

The sled needed a distance of 92.22 m and a time of 1.40 s to stop.

Step-by-step explanation:

The relationship between velocities and time is described by this equation:
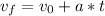`v_f=v_0+a*t`, where
`v_f` is the final velocity,
`v_0` is the initial velocity,
`a` the acceleration, and
`t` is the time during such acceleration is applied.

Solving the equation for the time, and applying to the case:
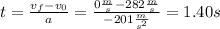`t=(v_f-v_0)/(a)=(0(m)/(s)-282(m)/(s)  )/(-201(m)/(s^2) )=1.40s`, where
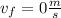`v_f=0(m)/(s)` because the sled is totally stopped,
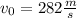`v_0=282(m)/(s)` is the velocity of the sled before braking and,
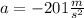`a=-201(m)/(s^2)` is negative because the deceleration applied by the brakes.

In the other hand, the equation that describes the distance in term of velocities and acceleration:
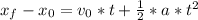`x_f-x_0=v_0*t+(1)/(2)*a*t^2`, where
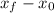`x_f-x_0` is the distance traveled,
`v_0` is the initial velocity,
`t` the time of the process and,
`a` is the acceleration of the process.

Then for this case the relationship becomes:
`x_f-x_0=282(m)/(s) *1.40s+(1)/(2)(-201(m)/(s))*(1.40s)^2=94.22m`.

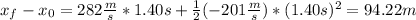Note that the acceleration is negative because is a braking process.

Answer 2

Answer:Stopping Distance= 197.82 m

Stopping time= 1.403 s

Explanation:

Given that:

• initial velocity, u=282
  `ms^(-1)`
• acceleration, a= -201
  `ms^(-2)`

• final velocity, v= 0
  `ms^(-1)` ∵ the body comes to the rest finally

To find:

• Stopping time, t
• stopping distance, s

From the given and asked data we identify the required equations of motion.

For calculating the stopping time:
`v=u+at` ⇒
`t=(v-u)/(t)`

`t=(0-282)/(-201) = 1.403 s`

For calculating the stopping distance:

`v^(2) =u^(2) +2as` ⇒
`s= (v^(2) -u^(2) )/(2a)`

putting the respective values

`s= (0^(2)-282^(2))/(2(-201)) = 197.82 m`