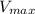Question

Consider a machine of mass 70 kg mounted to ground through an isolation system of total stiffness 30,000 N>m, with a measured damping ratio of 0.2. The machine produces a harmonic force of 450 N at 13 rad>s during steady-state operating conditions. Determine (a) the amplitude of motion of the machine, (b) the phase shift of the motion (with respect to a zero phase exciting force), (c) the transmissibility ratio, (d) the maximum dynamic force transmitted to the floor, and (e) the maximum velocity of the machine.

Answer 1

a)0.0229 m

b)0.393 rad

c)1.57

d)707.6 N

e)0.298 m/s

Step-by-step explanation:

Given:

• Mass of the machine, m=70 kg
• Stiffness of the system, k=30000 N/m
• Damping ratio=0.2
• Damping force, F=450 N
• Angular velocity
  `\omega=13\ \rm rad/s`

a)We know that the amplitude X at steady state is given by

`X=((F_0)/(m))/(√(\omega_n^2-\omega^2)^2 +(2\rho \omega_n\omega)^2))\\`

Where

• 
  `\omega_n=\sqrt{(k)/(m)}\\\\=\sqrt{(30000)/(70)}\\\\=20.7\ \rm rad/s`

• 
  `\omega=13\ \rm rad/s`
• 
  `\rho=0.2`

• 
  `F_0=450\ \rm N`
• 
  `m=70\ \rm kg`

`X=((450)/(70))/(√(20.7^2-13^2)^2 +(2* 0.2*20.7*13)^2))\\[tex]X=0.0229\ \rm m`

b) The phase shift of the motion is given by

`\tan\phi=(2\rho \omega_n \omega )/(\omega_n^2-\omega^2)\\\\(2*0.2*20.7*13 )/(20.7^2-\13^2)\\\\\phai=0.393\\`

c)Transmissibility ratio is given by

`T.R.=\sqrt{\frac{1+(2\rho r)^2}{(1-r^2)^2+{(2\rho r)^2}}}\\\\T.R.=\sqrt{\frac{1+(2*0.2*0.628)^2}{(1-0.628^2)^2+{(2*0.2*0/628)^2}}}\\\\=1.57`

d)The magnitude of the force transmitted to the ground is

`F_T=(T.R)* F_0\\\\=450*1.57\\\\=707.6\ \rm N`

e)The maximum velocity is given by
`V_(max)`

`V_(max)=\omega A_0\\\\=13* 0.0229\\\\=0.298\ \rm m/s`